Geometry Evaluation

Geometry Traversal

•

A simple rectangular face has one contour and four edges.

•

A contour will traverse a boundary so that the part face is always on the right-hand side (RHS). For an external contour the direction of traversal is clockwise. For an internal contour the direction of traversal is counterclockwise.

•

If a part is extruded from a sketch that has a U-shaped cross section there will be separate surfaces at each leg of the U-channel.

•

If a part is extruded from a sketch that has a square-shaped cross section, and a slot feature is then cut into the part to make it look like a U-channel, there will be one surface across the legs of the U-channel. The original surface of the part is represented as one surface with a cut through it.

Geometry Terms

Following are definitions for some geometric terms:

•

Surface—An ideal geometric representation, that is, an infinite plane.

•

Face—A trimmed surface. A face has one or more contours.

•

Contour—A closed loop on a face. A contour consists of multiple edges. A contour can belong to one face only.

•

Edge—The boundary of a trimmed surface.

An edge of a solid is the intersection of two surfaces. The edge belongs to those two surfaces and to two contours. An edge of a datum surface can be either the intersection of two datum surfaces or the external boundary of the surface.

If the edge is the intersection of two datum surfaces it will belong to those two surfaces and to two contours. If the edge is the external boundary of the datum surface it will belong to that surface alone and to a single contour.

Traversing the Geometry of a Solid Block

Methods Introduced:

pfcModelItemOwner.ListItems()

pfcSurface.ListContours()

pfcContour.ListElements()

To traverse the geometry, follow these steps:

Starting at the top-level model, use pfcModelItemOwner.ListItems() with an argument of ITEM_SURFACE.

Use pfcSurface.ListContours() to list the contours contained in a specified surface.

Use pfcContour.ListElements() to list the edges contained in the contour.

Curves and Edges

Datum curves, surface edges, and solid edges are represented in the same way in Web.Link. You can get edges through geometry traversal or get a list of edges using the methods presented in the section ModelItem.

The t Parameter

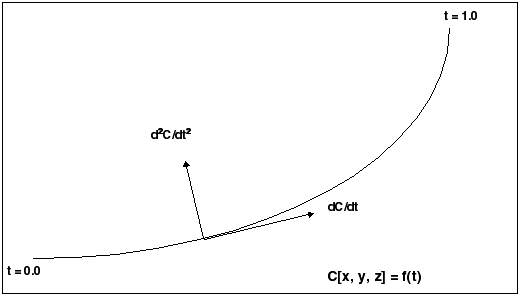
The geometry of each edge or curve is represented as a set of three parametric equations that represent the values of x, y, and z as functions of an independent parameter, t. The t parameter varies from 0.0 at the start of the curve to 1.0 at the end of it.

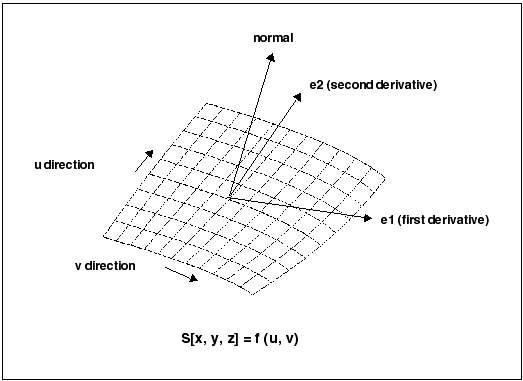
The following figure illustrates curve and edge parameterization.

Curve and Edge Types

Solid edges and datum curves can be any of the following types:

•

LINE—A straight line represented by the class pfcLine.

•

ARC—A circular curve represented by the class pfcArc.

•

SPLINE—A nonuniform cubic spline, represented by the class pfcSpline.

•

B-SPLINE—A nonuniform rational B-spline curve or edge, represented by the class pfcBSpline.

•

COMPOSITE CURVE—A combination of two or more curves, represented by the class pfcCompositeCurve. This is used for datum curves only.

See the section Geometry Representations for the parameterization of each curve type. To determine what type of curve a pfcEdge or pfcCurve object represents, use the Java instanceof operator.

Because each curve class inherits from pfcGeomCurve, you can use all the evaluation methods in pfcGeomCurve on any edge or curve.

The following curve types are not used in solid geometry and are reserved for future expansion:

•

CIRCLE (pfcCircle)

•

ELLIPSE (pfcEllipse)

•

POLYGON (pfcPolygon)

•

ARROW (pfcArrow)

•

TEXT (pfcText)

Evaluation of Curves and Edges

Methods Introduced:

pfcGeomCurve.Eval3DData()

pfcGeomCurve.EvalFromLength()

pfcGeomCurve.EvalParameter()

pfcGeomCurve.EvalLength()

pfcGeomCurve.EvalLengthBetween()

The methods in pfcGeomCurve provide information about any curve or edge.

The method pfcGeomCurve.Eval3DData() returns a pfcCurveXYZData object with information on the point represented by the input parameter t. The method pfcGeomCurve.EvalFromLength() returns a similar object with information on the point that is a specified distance from the starting point.

The method pfcGeomCurve.EvalParameter() returns the t parameter that represents the input pfcPoint3D object.

Both pfcGeomCurve.EvalLength() and pfcGeomCurve.EvalLengthBetween() return numerical values for the length of the curve or edge.

Solid Edge Geometry

Methods and Properties Introduced:

pfcEdge.Surface1

pfcEdge.Surface2

pfcEdge.Edge1

pfcEdge.Edge2

pfcEdge.EvalUV()

pfcEdge.GetDirection()

Note

The methods in the interface pfcEdge provide information only for solid or surface edges.

The properties pfcEdge.Surface1 and pfcEdge.Surface2 return the surfaces bounded by this edge. The properties pfcEdge.Edge1 and pfcEdge.Edge2 return the next edges in the two contours that contain this edge.

The method pfcEdge.EvalUV() evaluates geometry information based on the UV parameters of one of the bounding surfaces.

The method pfcEdge.GetDirection() returns a positive 1 if the edge is parameterized in the same direction as the containing contour, and –1 if the edge is parameterized opposite to the containing contour.

Curve Descriptors

A curve descriptor is a data object that describes the geometry of a curve or edge. A curve descriptor describes the geometry of a curve without being a part of a specific model.

Methods Introduced:

pfcGeomCurve.GetCurveDescriptor()

pfcGeomCurve.GetNURBSRepresentation()

Note

To get geometric information for an edge, access the pfcCurveDescriptor object for one edge using pfcGeomCurve.GetCurveDescriptor().

The method pfcGeomCurve.GetCurveDescriptor() returns a curve’s geometry as a data object.

The method pfcGeomCurve.GetNURBSRepresentation() returns a Non-Uniform Rational B-Spline Representation of a curve.

Contours

Methods and Properties Introduced:

pfcSurface.ListContours()

pfcContour.InternalTraversal

pfcContour.FindContainingContour()

pfcContour.EvalArea()

pfcContour.EvalOutline()

pfcContour.VerifyUV()

Contours are a series of edges that completely bound a surface. A contour is not a pfcModelItem. You cannot get contours using the methods that get different types of pfcModelItem. Use the method pfcSurface.ListContours() to get contours from their containing surfaces.

The property pfcContour.InternalTraversal returns a pfcContourTraversal enumerated type that identifies whether a given contour is on the outside or inside of a containing surface.

Use the method pfcContour.FindContainingContour() to find the contour that entirely encloses the specified contour.

The method pfcContour.EvalArea() provides the area enclosed by the contour.

The method pfcContour.EvalOutline() returns the points that make up the bounding rectangle of the contour.

Use the method pfcContour.VerifyUV() to determine whether the given pfcUVParams argument lies inside the contour, on the boundary, or outside the contour.

Surfaces

Using Web.Link you access datum and solid surfaces in the same way.

UV Parameterization

A surface in Creo Parametric is described as a series of parametric equations where two parameters, u and v, determine the x, y, and z coordinates. Unlike the edge parameter, t, these parameters need not start at 0.0, nor are they limited to 1.0.

The figure on the following page illustrates surface parameterization.

Surface Types

Surfaces within Creo Parametric can be any of the following types:

•

PLANE—A planar surface represented by the class pfcPlane.

•

CYLINDER—A cylindrical surface represented by the class pfcCylinder.

•

CONE—A conic surface region represented by the class pfcCone.

•

TORUS—A toroidal surface region represented by the class pfcTorus.

•

REVOLVED SURFACE—Generated by revolving a curve about an axis. This is represented by the class pfcRevSurface.

•

RULED SURFACE—Generated by interpolating linearly between two curve entities. This is represented by the class pfcRuledSurface.

•

TABULATED CYLINDER—Generated by extruding a curve linearly. This is represented by the class pfcTabulatedCylinder.

•

COONS PATCH—A coons patch is used to blend surfaces together. It is represented by the class pfcCoonsPatch.

•

FILLET SURFACE—A filleted surface is found where a round or fillet is placed on a curved edge or an edge with a non-consistant arc radii. On a straight edge a cylinder is used to represent a fillet. This is represented by the class pfcFilletedSurface.

•

SPLINE SURFACE— A nonuniform bicubic spline surface that passes through a grid with tangent vectors given at each point. This is represented by the class pfcSplineSurface.

•

NURBS SURFACE—A NURBS surface is defined by basic functions (in u and v), expandable arrays of knots, weights, and control points. This is represented by the class pfcNURBSSurface.

•

CYLINDRICAL SPLINE SURFACE— A cylindrical spline surface is a nonuniform bicubic spline surface that passes through a grid with tangent vectors given at each point. This is represented by the class pfcCylindricalSplineSurface.

To determine which type of surface a pfcSurface object represents, access the surface type using pfcSurface.GetSurfaceType.

Surface Information

Methods Introduced:

pfcSurface.GetSurfaceType()

pfcSurface.GetXYZExtents()

pfcSurface.GetUVExtents()

pfcSurface.GetOrientation()

The method pfcSurface.GetSurfaceType() returns the type of the surface using the enumerated data type pfcSurfaceType and the valid values are:

•

SURFACE_PLANE

•

SURFACE_CYLINDER

•

SURFACE_CONE

•

SURFACE_TORUS

•

SURFACE_RULED

•

SURFACE_REVOLVED

•

SURFACE_TABULATED_CYLINDER

•

SURFACE_FILLET

•

SURFACE_COONS_PATCH

•

SURFACE_SPLINE

•

SURFACE_NURBS

•

SURFACE_CYLINDRICAL_SPLINE

•

SURFACE_FOREIGN

•

SURFACE_SPL2DER

The method pfcSurface.GetXYZExtents() returns the XYZ points at the corners of the surface.

The method pfcSurface.GetUVExtents() returns the UV parameters at the corners of the surface.

The method pfcSurface.GetOrientation() returns the orientation of the surface using the enumerated data type pfcSurfaceOrientation and the valid values are:

•

SURFACEORIENT_NONE—Surface that does not need orientation. For example, a solid surface needs orientation and therefore cannot be specified.

•

SURFACEORIENT_OUTWARD—Surface that has oriented outward away from the solid model. du X dv points outward.

•

SURFACEORIENT_INWARD—Surface that has oriented inward toward the solid model. du X dv points inward.

Evaluation of Surfaces

Surface methods allow you to use multiple surface information to calculate, evaluate, determine, and examine surface functions and problems.

Methods and Properties Introduced:

pfcSurface.OwnerQuilt

pfcSurface.EvalClosestPoint()

pfcSurface.EvalClosestPointOnSurface()

pfcSurface.Eval3DData()

pfcSurface.EvalParameters()

pfcSurface.EvalArea()

pfcSurface.EvalDiameter()

pfcSurface.EvalPrincipalCurv()

pfcSurface.VerifyUV()

pfcSurface.EvalMaximum()

pfcSurface.EvalMinimum()

pfcSurface.ListSameSurfaces()

The property pfcSurface.OwnerQuilt returns the pfcQuilt object that contains the datum surface.

The method pfcSurface.EvalClosestPoint() projects a three-dimensional point onto the surface. Use the method pfcSurface.EvalClosestPointOnSurface() to determine whether the specified three-dimensional point is on the surface, within the accuracy of the part. If it is, the method returns the point that is exactly on the surface. Otherwise the method returns null.

The method pfcSurface.Eval3DData() returns a pfcSurfXYZData object that contains information about the surface at the specified u and v parameters. The method pfcSurface.EvalParameters() returns the u and v parameters that correspond to the specified three-dimensional point.

The method pfcSurface.EvalArea() returns the area of the surface, whereas pfcSurface.EvalDiameter() returns the diameter of the surface. If the diameter varies the optional pfcUVParams argument identifies where the diameter should be evaluated.

The method pfcSurface.EvalPrincipalCurv() returns a pfcCurvatureData object with information regarding the curvature of the surface at the specified u and v parameters.

Use the method pfcSurface.VerifyUV() to determine whether the pfcUVParams are actually within the boundary of the surface.

The methods pfcSurface.EvalMaximum() and pfcSurface.EvalMinimum() return the three-dimensional point on the surface that is the furthest in the direction of (or away from) the specified vector.

The method pfcSurface.ListSameSurfaces() identifies other surfaces that are tangent and connect to the given surface.

Surface Descriptors

A surface descriptor is a data object that describes the shape and geometry of a specified surface. A surface descriptor allows you to describe a surface in 3D without an owner ID.

Methods Introduced:

pfcSurface.GetSurfaceDescriptor()

pfcSurface.GetNURBSRepresentation()

The method pfcSurface.GetSurfaceDescriptor() returns a surfaces geometry as a data object.

The method pfcSurface.GetNURBSRepresentation() returns a Non-Uniform Rational B-Spline Representation of a surface.

Axes, Coordinate Systems, and Points

Coordinate axes, datum points, and coordinate systems are all model items. Use the methods that return pfcModelItems to get one of these geometry objects. Refer to the section ModelItem for additional information.

Evaluation of ModelItems

Properties Introduced:

pfcAxis.Surf

pfcCoordSystem.CoordSys

pfcPoint.Point

The property pfcAxis.Surf returns the revolved surface that uses the axis.

The property pfcCoordSystem.CoordSys returns the pfcTransform3D object (which includes the origin and x-, y-, and z- axes) that defines the coordinate system.

The property pfcPoint.Point returns the xyz coordinates of the datum point.

Interference

Creo Parametric assemblies can contain interferences between components when constraint by certain rules defined by the user. The pfcInterference module allows the user to detect and analyze any interferences within the assembly. The analysis of this functionality should be looked at from two standpoints: global and selection based analysis.

Methods and Properties Introduced:

MpfcInterference.CreateGlobalEvaluator()

pfcGlobalEvaluator.ComputeGlobalInterference()

pfcGlobalEvaluator.Assem

pfcGlobalInterference.Volume

pfcGlobalInterference.SelParts

To compute all the interferences within an Assembly one has to call MpfcInterference.CreateGlobalEvaluator() with a pfcAssembly object as an argument. This call returns apfcGlobalEvaluator object.

The property pfcGlobalEvaluator.Assem accesses the assembly to be evaluated .

The method pfcGlobalEvaluator.ComputeGlobalInterference() determines the set of all the interferences within the assembly.

This method will return a sequence of pfcGlobalInterference objects or null if there are no interfering parts. Each object contains a pair of intersecting parts and an object representing the interference volume, which can be extracted by using pfcGlobalInterference.SelParts and pfcGlobalInterference.Volume respectively.

Analyzing Interference Information

Methods and Properties Introduced:

pfcSelectionPair.Create()

MpfcInterference.CreateSelectionEvaluator()

pfcSelectionEvaluator.Selections

pfcSelectionEvaluator.ComputeInterference()

pfcSelectionEvaluator.ComputeClearance()

pfcSelectionEvaluator.ComputeNearestCriticalDistance()

The method pfcSelectionPair.Create() creates a pfcSelectionPair object using two pfcSelection objects as arguments.

A return from this method will serve as an argument to MpfcInterference.CreateSelectionEvaluator(), which will provide a way to determine the interference data between the two selections.

pfcSelectionEvaluator.Selections will extract and set the object to be evaluated.

pfcSelectionEvaluator.ComputeInterference() determines the interfering information about the provided selections. This method will return the pfcInterferenceVolume object or null if the selections do no interfere.

pfcSelectionEvaluator.ComputeClearance() computes the clearance data for the two selection. This method returns a pfcClearanceData object, which can be used to obtain and set clearance distance, nearest points between selections, and a boolean IsInterferening variable.

pfcSelectionEvaluator.ComputeNearestCriticalDistance() finds a critical point of the distance function between two selections.

This method returns a pfcCriticalDistanceData object, which is used to determine and set critical points, surface parameters, and critical distance between points.

Analyzing Interference Volume

Methods and Properties Introduced:

pfcInterferenceVolume.ComputeVolume()

pfcInterferenceVolume.Highlight()

pfcInterferenceVolume.Boundaries

The method pfcInterferenceVolume.ComputeVolume() will calculate a value for interfering volume.

The method pfcInterferenceVolume.Highlight() will highlight the interfering volume with the color provided in the argument to the function.

The property pfcInterferenceVolume.Boundaries will return a set of boundary surface descriptors for the interference volume.

Example Code

The sample code in the file pfcInterferenceExamples.js located at Web.Link <creo_weblink_loadpoint>/weblinkexamples/jscript finds the interference in an assembly, highlights the interfering surfaces, and highlights calculates the interference volume.

This application finds the interference in an assembly, highlights the interfering surfaces, and highlights calculates the interference volume.

This method allows a user to evaluate the assembly for a presence of any interferences. Upon finding one, this method will highlight the interfering surfaces, compute and highlight the interference volume.